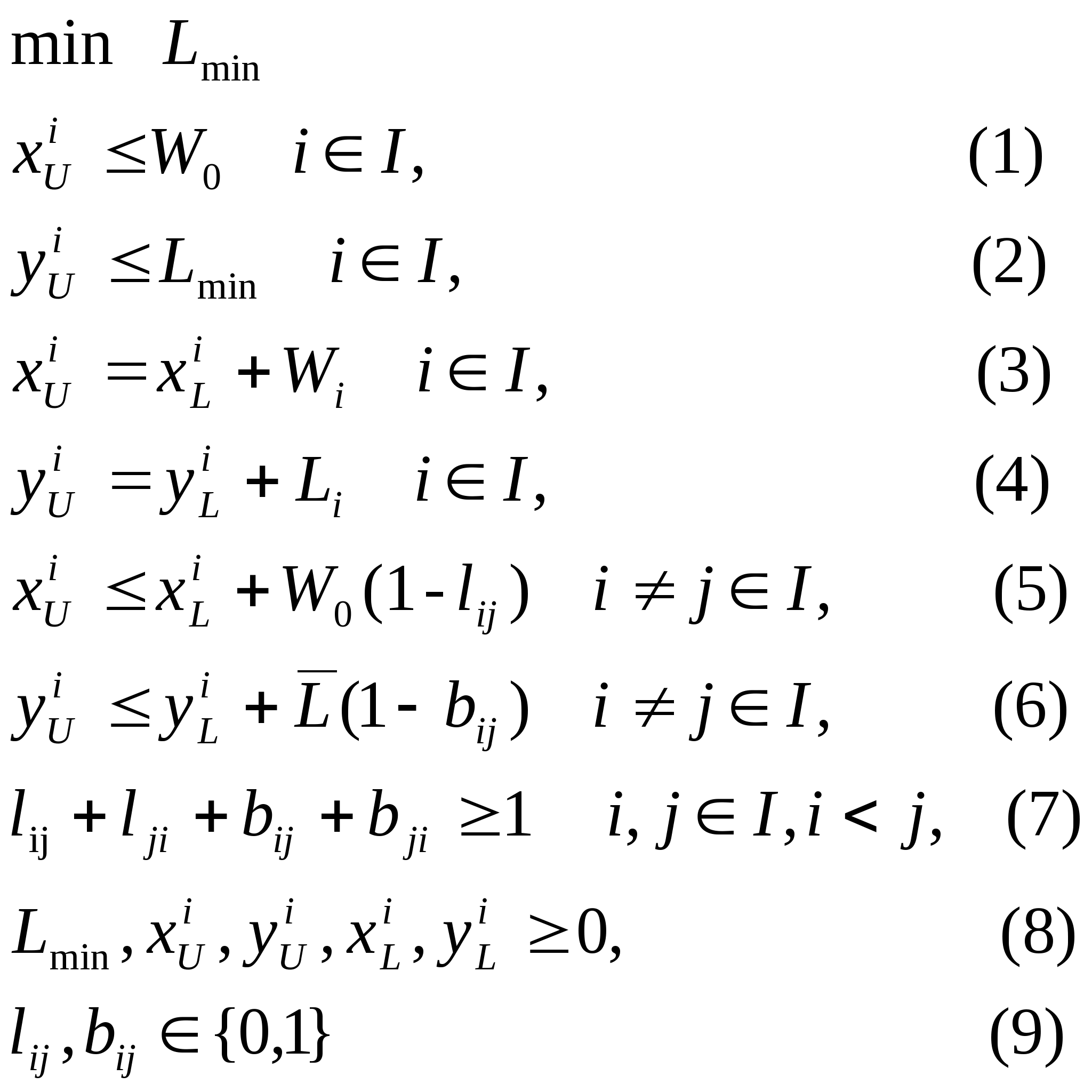Trabalho de Tópicos Avançados em Sistemas de Computação

Programação Linear e Inteira

Obtenção de Soluções Ótimas para o Problema de Strip Packing

O problema de corte ou empacotamento bidimensional pode ser descrito como o problema de cortar um conjunto de peças retangulares a partir de uma única peça retangular maior com o objetivo de minimizar os gastos ou ajustar as perdas. Os problemas de corte e empacotamento são de especial interesse para as indústrias têxtil, papel, metal e plástico, além de situações onde há necessidade de realizar escalonamento com restrição de recursos.

Neste trabalho, atuaremos sobre um caso especial do problema de corte bidimensional, denominado strip-packing com cortes não guilhotinados. Nesse problema, a entrada consiste em uma lista R=(R₁,...,R_n) de n retângulos, cada uma tendo uma largura não maior que W₀. Os retângulos são empacotados em um strip de largura W₀ de forma que:

• Retângulos não se sobrepõem e nem são colocados sobre as bordas do strip.

• Os retângulos têm que ser empacotados com seus lados paralelos para as bordas do strip.

• O tamanho do empacotamento deve ser minimizado, isto é, o gasto com o empacotamento tem que ser minimizado.

Um i-ésimo retângulo é dado por R_i=(W_i,L_i) onde W_i e L_i são a largura e tamanho de R_i. Apresenta-se a seguir uma formulação matemática para o problema strip-packing.

• I={1,...,n} conjunto de índices dos retângulos

• L_min= tamanho do strip (faixa/rolo) a ser minimizado

• xⁱ_L= coordenada x da parte inferior esquerda de R_i

• yⁱ_L= coordenada y da parte inferior esquerda de R_i

• xⁱ_U= coordenada x da parte superior direita de R_i

• yⁱ_U= coordenada y da parte superior direita de R_i

• l_ij=1 se R_i é colocado à esquerda de R_j, ou 0 caso contrário

• b_ij=1 se R_i é colocado abaixo de R_j, ou 0 caso contrário

• =algum limite superior conhecido em L_min (parâmetro).

O problema pode ser formulado como:

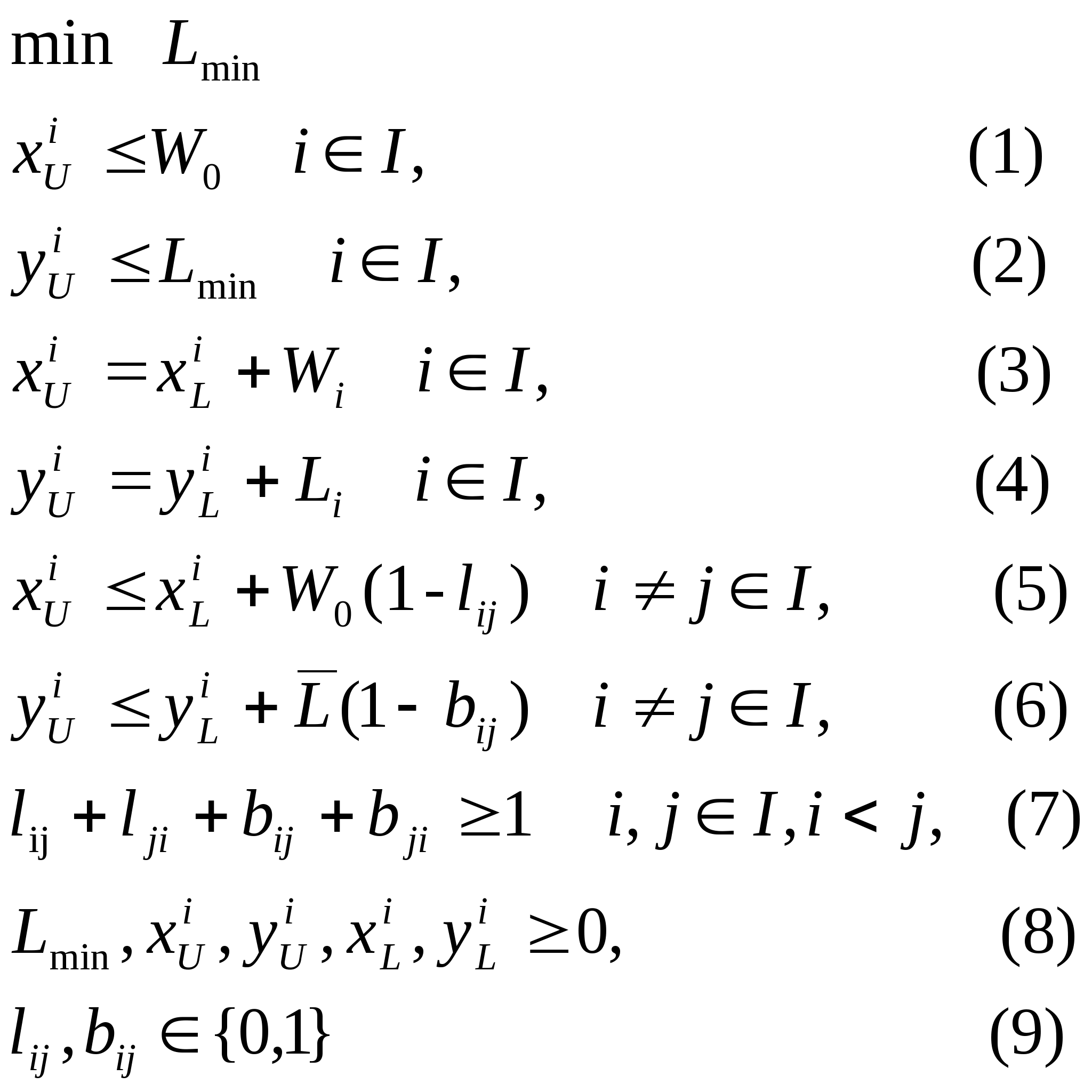
A restrição (1) garante que R_i não sobrepõe a borda direita do strip. A restrição (2) força L_min a ser do tamanho de, pelo menos, cada retângulo. Restrições (3 ) e (4) forçam um relacionamento entre as coordenadas inferiores e superiores de cada retângulo. Em outras palavras, a restrição (3) indica que a coordenada que representa a largura da parte superior do retângulo deve ser igual à soma da coordenada que representa o início da largura do retângulo (largura inferior) mais a largura do retângulo. O mesmo raciocínio vale para o tamanho do retângulo (Restrição (4)). A Restrição (5) garante que a borda direita de R_i está localizada à esquerda de R_j se l_ij é igual a 1. A Restrição (6) garante que R_i está localizado abaixo de R_j se b_ij é igual a 1. A Restrição (7) evita que R_i e R_j se sobrepõem pois requer que R_i seja localizado à esquerda de R_j ou R_j seja localizado à esquerda de R_i, ou R_i seja localizado abaixo de R_j ou R_j é localizado abaixo de R_i. A Restrição (8) é restrição de não-negatividade e a restrição (9) é chamada de restrição binária.

Objetivo do Trabalho

• Desenvolver uma implementação para o problema supramencionado de maneira a fornecer soluções ótimas para instâncias do problema de strip-packing.

Metodologia para Desenvolvimento do Trabalho

• Trabalho pode ser desenvolvido em duplas ou individualmente.

• Entender o problema e o modelo matemático que representa.

• Adotar uma técnica de resolução (algoritmo exato, heurística, técnica de PL, técnica de PI).

• Se for necessário, reformulá-lo de maneira a adequar às limitações das ferramentas e/ou técnicas adotadas.

• Testar a técnica implementada com instâncias de testes de strip-packing em: http://dip.sun.ac.za/~vuuren/repositories/levelpaper/spp%5B1%5D.htm

• A maior parte das instâncias de testes para problemas strip-packing possuem um formato que segue o padrão

Nº de RETANGULOS LARGURA DO STRIP

1 TAMANHO_RET_1 LARGURA_RET_1

2 TAMANHO_RET_2 LARGURA_RET_2

...

N TAMANHO_RET_N LARGURA_RET_N

Notas do Trabalho, Datas e Esclarecimento de Dúvidas

• O trabalho terá peso três na atribuição da média final da disciplina (MF=(P1*3.5+P2*3.5+T1*3)+Bônus)

• O Bônus é um valor entre 0<=Bônus<=1.5 e corresponde à participação nas atividades da disciplina, resolução das listas de exercícios, qualidade na resolução e encaminhamento do trabalho.

• Esse trabalho não terá checkpoints no decorrer do semestre. No entanto, algumas aulas PODERÃO ser dedicadas para sua resolução. Nesses casos, o professor solicitará um relatório (simples e escrito à mão) sobre as atividades desenvolvidas em sala de aula.

  • Em caso de dúvidas ou esclarecimentos sobre o trabalho, os alunos devem procurar o Professor após as aulas da disciplina e/ou enviar e-mail com o assunto: TASC: Dúvidas – Trabalho1.

• Na entrega do trabalho, a dupla (ou o acadêmico) deverá entregar a implementação realizada e um relatório de no máximo 08 páginas indicando como resolveu o problema, quais ferramentas foram utilizadas, quais foram os resultados alcançados de acordo com as instâncias de testes e qual foi a bibliografia consultada. O relatório deve seguir o formato disponível aqui.

• IMPORTANTE: A data de entrega do trabalho é dia 23/06.